Cara Mencari Luas Segitiga Diketahui Panjang Sisi

Hei semua. Ketemu lagi sama aye, Mas Wody. Untuk postingan kali ini, aye akan menjelaskan tentang bagaimana cara mencari luas segitiga tapi yang diketahui panjang sisi-sisinya bukan tinggi segitiganya ^_^ Langsung saja kita mulai pembahasannya.












Mencari luas segitiga sebenarnya sangatlah mudah. Seperti yang kita ketahui bahwa rumus luas segitiga adalah alas dikali dengan tinggi lalu dibagi dua.

Rumus yang sangat mudah kan? Pasti kalian udah pada hafal mati sama rumus ini. Akan tetapi, rumus tersebut hanya berguna apabila tinggi segitiga tersebut diketahui. Lalu, bagaimana kalau tinggi segitiganya tidak diketahui? Bagaimana cara mencari luas segitiganya? Nah, mari kita cari tau sama-sama caranya.

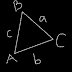
Pertama-tama mari kita gambar segitiga ABC lalu kita simbolkan sisi yang berhadapan dengan setiap sudut dengan huruf kecilnya yakni sisi a, b, dan c.

Misalkan panjang a, b, dan c diketahui. Untuk mencari luasnya tentu saja kita harus cari dulu tingginya. Pertama-tama pilih sisi yang akan dijadikan alas. Lalu tarik garis dari sudut yang berhadapan dengan sisi yang dipilih tadi tegak lurus dengan sisi tersebut. Nah, garis tersebutlah yang dijadikan sebagai tinggi. Di postingan ini, aye akan memilih sisi c sebagai alas karena memang kebetulan posisinya ada di bagian bawah pada gambar. Garis tinggi tersebut aye simbolkan dengan t.

Lalu, bagaimana caranya untuk mencari nilai t? Kita bisa mencari nilai t dengan menggunakan rumus sinus. Perhatikan gambar, dengan menggunakan sinus, kita bisa memperoleh nilai t apabila sudut A atau B diketahui. Jadi, t = bsin∠A atau t = asin∠B. Untuk kali ini, aye pilih aja yang t = bsin∠A aja.

Sekarang, yang menjadi masalah kita tidak tau berapa besar sudut ∠A. Padahal kalau kita sudah tahu besar sudut ∠A, kita sudah pasti bisa mencari nilai sinusnya. Sebenarnya, kita bisa menemukan besar sudut ∠A dengan menggunakan rumus kosinus.

Nah, sekarang kita sudah menemukan nilai kosinus dari sudut ∠A. Pastinya sangat mudah untuk memperoleh nilai sinusnya dengan menggunakan identitas trigonometri.

Dengan menggunakan identitas trigonometri di atas, kita bisa memperoleh nilai sin∠A dengan mudah. Lalu, setelah itu, kita bisa mencari tingginya, lalu luasnya. Walla~ selesai. Eits, tunggu dulu. Sebenarnya kita masih bisa mengembangkan rumus ini sehingga muncul rumus baru yang bisa kita gunakan terus tanpa perlu embel-embel mencari nilai sudut sama tinggi.

Perhatikan kembali rumus identitas trigonometri.

Mari kita faktorkan 1 - cos²∠A dengan menggunakan rumus selisih kuadrat. Jadi,
1 - cos²∠A difaktorkan menjadi (1 + cos∠A)(1 - cos∠A).

 

Nah, selanjutnya, kita ubah cos∠A dengan ekspresi yang hanya terdiri atas a, b, dan c dengan menggunakan aturan kosinus tadi.

Next, yang kita perlu lakukan adalah pemanipulasian aljabar.

Nah, skarang sin²∠A sudah didapat. Untuk memperoleh sin∠A, qta hanya perlu menarik akar. Mengingat 0° < ∠A < 180°, itu artinya sin∠A > 0 karena berada di kuadran pertama atau kedua. Itu artinya, qta tidak perlu pake tanda plus-minus (±) sehingga langsung aja qta tarik akar positif.

Sekarang, qta kembali lagi ke rumus luas segitiga.

Ingat bahwa t = bsin∠A.

Dan tadi, kita juga sudah berhasil menemukan sin∠A. Tinggal substitusikan saja.

Yap, itulah rumus luasnya apabila diketahui panjang sisi-sisinya. Hanya sampe disitu? Yap, sebenarnya hanya sampe disitu, tapi rumus ini bisa diringkas lho.

Misalkan K adalah keliling segitiga, berarti K = a + b + c. Sekarang, kita misalkan S adalah setengah dari keliling, itu artinya S = K/2 = (a + b + c)/2. Nah, dengan S ini kita bisa menyingkat bagian dalam akar. Mari kita telaah satu persatu setiap faktor yang ada di dalam akar

(a + b + c) = K =  2S
(b + c - a) = b + c + a - 2a = K - 2a = 2S - 2a = 2(S - a)
(a + b - c) = a + b + c - 2c = K - 2c = 2S - 2b = 2(S - c)
(a + c - b) = a + c + b - 2b = K - 2b = 2S - 2b = 2(S - b)

Itu artinya, kita bisa meringkas rumusnya sebagai berikut:

Yap, pada akhirnya rumus mencari luas segitiga diketahui panjang sisi adalah sebagai berikut (biarkan aye paparkan lagi).

Yap, itulah rumus yang bisa kita gunakan untuk mencari luas segitiga yang diketahui hanya panjang sisi, bukan tinggi. Sekarang, kita bisa mencari luas segitiga hanya menggunakan rumus tersebut. Kalau ada yang mau ditanyakan, silahkan ditanyakan di kolom komentar. Kalau ada kesalahan, silahkan dikoreksi. Sampai ketemu lagi di postingan selanjutnya. Da da~